Ref: Single Supply Op-Amp Circuit Collection (ti application note SLOA058)
1 Introduction
There have been many excellent collections of op-amp circuits in the past, but all of them focus exclusively on split-supply circuits. Many times, the designer who has to operate a circuit from a single supply does not know how to do the conversion.
Single-supply operation requires a little more care than split-supply circuits. The designer should read and understand this introductory material.
1.1 Split Supply vs Single Supply
All op amps have two power pins. In most cases, they are labeled VCC+ and VCC-, but sometimes they are labeled VCC and GND. This is an attempt on the part of the data sheet author to categorize the part as a split-supply or single-supply part. However, it does not mean that the op amp has to be operated that way— it may or may not be able to operate from different voltage rails. Consult the data sheet for the op amp, especially the absolute maximum ratings and voltage-swing specifications, before operating at anything other than the recommended power-supply voltage(s).
Most analog designers know how to use op amps with a split power supply. As shown in the left half of Figure 1, a split power supply consists of a positive supply and an equal and opposite negative supply. The most common values are ±15 V, but ±12 V and ±5 V are also used. The input and output voltages are referenced to ground, and swing both positive and negative to a limit of VOM±, the maximum peak-output voltage swing.
A single-supply circuit (right side of Figure 1) connects the op-amp power pins to a positive voltage and ground. The positive voltage is connected to VCC+, and ground is connected to VCCor GND. A virtual ground, halfway between the positive supply voltage and ground, is the reference for the input and output voltages. The voltage swings above and below this virtual ground to the limit of VOM±. Some newer op amps have different high- and low-voltage rails, which are specified in data sheets as VOH and VOL, respectively. It is important to note that there are very few cases when the designer has the liberty to reference the input and output to the virtual ground. In most cases, the input and output will be referenced to system ground, and the designer must use decoupling capacitors to isolate the dc potential of the virtual ground from the input and output.

A common value for single supplies is 5 V, but voltage rails are getting lower, with 3 V and even lower voltages becoming common. Because of this, single-supply op amps are often rail-to-rail devices, which avoids losing dynamic range. Rail-to-rail may or may not apply to both the input and output stages. Be aware that even though a device might be specified as rail-to-rail, some specifications can degrade close to the rails. Be sure to consult the data sheet for complete specifications on both the inputs and outputs. It is the designer’s obligation to ensure that the voltage rails of the op amp do not degrade the system specifications.
1.2 Virtual Ground
Single-supply operation requires the generation of a virtual ground, usually at a voltage equal to Vcc/2. The circuit in Figure 2 can be used to generate Vcc/2, but its performance deteriorates at low frequencies.
R1 and R2 are equal values, selected with power consumption vs allowable noise in mind. Capacitor C1 forms a low-pass filter to eliminate conducted noise on the voltage rail. Some applications can omit the buffer op amp.
In what follows, there are a few circuits in which a virtual ground has to be introduced with two resistors within the circuit because one virtual ground is not suitable. In these instances, the resistors should be 100 kW or greater; when such a case arises, values are indicated on the schematic.
1.3 AC-Coupling
A virtual ground is at a dc level above system ground; in effect, a small, local-ground system has been created within the op-amp stage. However, there is a potential problem: the input source and output load are probably referenced to system ground, and if the op-amp stage is connected to a source that is referenced to ground instead of virtual ground, there will be an unacceptable dc offset. If this happens, the op amp becomes unable to operate on the input signal, because it must then process signals at and below its input and output rails.
The solution is to ac-couple the signals to and from the op-amp stage. In this way, the input and output devices can be referenced to ground, and the op-amp circuitry can be referenced to a virtual ground.
When more than one op-amp stage is used, interstage decoupling capacitors might become unnecessary if all of the following conditions are met:
· The first stage is referenced to virtual ground.
· The second stage is referenced to virtual ground.
· There is no gain in either stage. Any dc offset in either stage is multiplied by the gain in both, and probably takes the circuit out of its normal operating range.
If there is any doubt, assemble a prototype including ac-coupling capacitors, then remove them one at a time. Unless the input or output are referenced to virtual ground, there must be an input-decoupling capacitor to decouple the source and an output-decoupling capacitor to decouple the load. A good troubleshooting technique for ac circuits is to terminate the input and output, then check the dc voltage at all op-amp inverting and noninverting inputs and at the op-amp outputs. All dc voltages should be very close to the virtual-ground value. If they are not, decoupling capacitors are mandatory in the previous stage (or something is wrong with the circuit).
1.4 Combining Op-Amp Stages
Combining op-amp stages to save money and board space is possible in some cases, but it often leads to unavoidable interactions between filter response characteristics, offset voltages, noise, and other circuit characteristics. The designer should always begin by prototyping separate gain, offset, and filter stages, then combine them if possible after each individual circuit function has been verified. Unless otherwise specified, filter circuits included in this document are unity gain.
1.5 Selecting Resistor and Capacitor Values
The designer who is new to analog design often wonders how to select component values.Should resistors be in the 1-W decade or the 1-MW decade? Resistor values in the 1-kW to 100-kW range are good for general-purpose applications. High-speed applications usually use resistors in the 100-W to 1-kW decade, and they consume more power. Portable applications usually use resistors in the 1-MW or even 10-MW decade, and they are more prone to noise. Basic formulas for selecting resistor and capacitor values for tuned circuits are given in the various figures. For filter applications, resistors should be chosen from 1% E-96 values. Once the resistor decade range has been selected, choose standard E-12 value capacitors. Some tuned circuits may require E-24 values, but they should be avoided where possible. Capacitors with only 5% tolerance should be avoided in critical tuned circuits— use 1% instead.
2 Basic Circuits
2.1 Gain
Gain stages come in two basic varieties: inverting and noninverting. The ac-coupled version is shown in Figure 3. For ac circuits, inversion means an ac-phase shift of 180°. These circuits work by taking advantage of the coupling capacitor, CIN, to prevent the circuit from having dc gain. They have ac gain only. If CIN is omitted in a dc system, dc gain must be taken into account.
It is very important not to violate the bandwidth limit of the op amp at the highest frequency seen by the circuit. Practical circuits can include gains of 100 (40 dB), but higher gains could cause the circuit to oscillate unless special care is taken during PC board layout. It is better to cascade two or more equal-gain stages than to attempt high gain in a single stage.
2.2 Attenuation
The traditional way of doing inverting attenuation with an op-amp circuit is shown in Figure 4, in
which R2 < R1. This method is not recommended, because many op amps are unstable at gains of less than unity. The correct way to construct an attenuation circuit1 is shown in Figure 5.
To work with normalized values, do the following:
· Select a base-value of resistance, usually between 1 kW and 100 kW for Rf and Rin.
· Divide Rin in two for RinA and RinB.
· Multiply the base value for Rf and Rin by 1 or 2, as shown in Figure 5.
· Look up the normalization factor for R3 in the table below, and multiply it by the base-value
of resistance.
For example, if Rf is 20 kW, RinA and RinB are each 10 kW, and a 3-dB attenuator would use a
12.1-kW resistor.
Noninverting attenuation can be performed with a voltage divider and a noninverting buffer as
shown in Figure 6.
2.4 Difference Amplifier
Just as there are summing circuits, there are also subtracting circuits (Figure 8). A common application is to eliminate the vocal track (recorded at equal levels in both channels) from stereo recordings.
2.5 Simulated Inductor
The circuit in Figure 9 reverses the operation of a capacitor, thus making a simulated inductor. An inductor resists any change in its current, so when a dc voltage is applied to an inductance, the current rises slowly, and the voltage falls as the external resistance becomes more significant.
An inductor passes low frequencies more readily than high frequencies, the opposite of a capacitor. An ideal inductor has zero resistance. It passes dc without limitation, but it has infinite impedance at infinite frequency.
If a dc voltage is suddenly applied to the inverting input through resistor R1, the op amp ignores the sudden load because the change is also coupled directly to the noninverting input via C1.
The op amp represents high impedance, just as an inductor does. As C1 charges through R2, the voltage across R2 falls, so the op-amp draws current from the input through R1. This continues as the capacitor charges, and eventually the op-amp has an input and output close to virtual ground (Vcc/2). When C1 is fully charged, resistor R1 limits the current flow, and this appears as a series resistance within the simulated inductor. This series resistance limits the Q of the inductor. Real inductors generally have much less resistance than the simulated variety.
There are some limitations of a simulated inductor:
· One end of the inductor is connected to virtual ground.
· The simulated inductor cannot be made with high Q, due to the series resistor R1.
· It does not have the same energy storage as a real inductor.
The collapse of the magnetic field in a real inductor causes large voltage spikes of opposite polarity. The simulated inductor is limited to the voltage swing of the op amp, so the flyback pulse is limited to the voltage swing.
2.6 Instrumentation Amplifiers
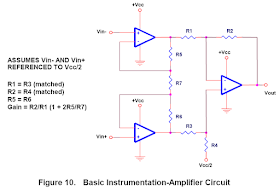
Instrumentation amplifiers are used whenever dc gain is needed on a low-level signal that would be loaded by conventional differential-amplifier topologies. Instrumentation amplifiers take advantage of the high input impedance of noninverting op-amp inputs. The basic instrumentation amplifier topology is shown in Figure 10.
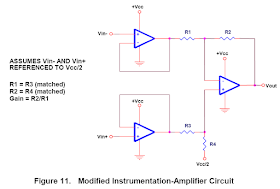
This circuit, and the other instrumentation amplifier topologies presented here, assume that the inputs are already referenced to half-supply. This is the case with strain gauges that are operated from Vcc. The basic disadvantage of this circuit is that it requires matched resistors; otherwise, it would suffer from poor CMRR (see for example, Op Amps for Everyone). The circuit in Figure 10 can be simplified by eliminating three resistors, as shown in Figure 11.
Here, the gain is easier to calculate, but a disadvantage is that now two resistors must be changed instead of one, and they must be matched resistors. Another disadvantage is that the first stage(s) cannot be used for gain. An instrumentation amplifier can also be made from two op amps; this is shown in Figure 12.
3 Filter Circuits
This section is devoted to op-amp active filters. In many cases, it is necessary to block dc voltage from the virtual ground of the op-amp stage by adding a capacitor to the input of the circuit. This capacitor forms a high-pass filter with the input so, in a sense, all these circuits have a high-pass characteristic. The designer must insure that the input capacitor is at least 100 times the value of the other capacitors in the circuit, so that the high-pass characteristic does not come into play at the frequencies of interest in the circuit. For filter circuits with gain, 1000 times might be better. If the input voltage already contains a Vcc/2 offset, the capacitor can be omitted. These circuits will have a half-supply dc offset at their output. If the circuit is the last stage in the system, an output-coupling capacitor may also be required. There are trade-offs involved in filter design. The most desirable situation is to implement a filter with a single op amp. Ideally, the filter would be simple to implement, and the designer would have complete control over:
· The filter corner / center frequency
· The gain of the filter circuit
· The Q of band-pass and notch filters, or style of low-pass and high-pass filter (Butterworth,
Chebyshev, or Bessell).
Unfortunately, such is not the case— complete control over the filter is seldom possible with a single op amp. If control is possible, it frequently involves complex interactions between passive components, and this means complex mathematical calculations that intimidate many designers. More control usually means more op amps, which may be acceptable in designs that will not be produced in large volumes, or that may be subject to several changes before the design is finalized. If the designer needs to implement a filter with as few components as possible, there will be no choice but to resort to traditional filter-design techniques and perform the necessary calculations.
3.1 Single Pole Circuits
Single-pole circuits are the simplest filter circuits. They have a roll off of 20 dB per decade.
3.1.1 Low Pass Filter Circuits
Typical low-pass filter circuits are shown in Figure 13.
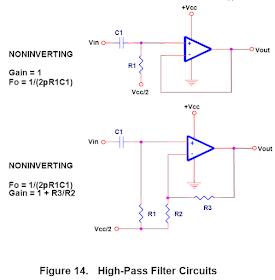
3.1.2 High Pass Filter Circuits
Typical high-pass filter circuits are shown in Figure 14.
3.1.3 All-Pass Filter
The all-pass filter passes all frequencies at the same gain. It is used to change the phase of the signal, and it can also be used as a phase-correction circuit. The circuit shown in Figure 15 has a 90° phase shift at F(90). At dc, the phase shift is 0°, and at high frequencies it is 180°
1 Introduction
There have been many excellent collections of op-amp circuits in the past, but all of them focus exclusively on split-supply circuits. Many times, the designer who has to operate a circuit from a single supply does not know how to do the conversion.
Single-supply operation requires a little more care than split-supply circuits. The designer should read and understand this introductory material.
1.1 Split Supply vs Single Supply
All op amps have two power pins. In most cases, they are labeled VCC+ and VCC-, but sometimes they are labeled VCC and GND. This is an attempt on the part of the data sheet author to categorize the part as a split-supply or single-supply part. However, it does not mean that the op amp has to be operated that way— it may or may not be able to operate from different voltage rails. Consult the data sheet for the op amp, especially the absolute maximum ratings and voltage-swing specifications, before operating at anything other than the recommended power-supply voltage(s).
Most analog designers know how to use op amps with a split power supply. As shown in the left half of Figure 1, a split power supply consists of a positive supply and an equal and opposite negative supply. The most common values are ±15 V, but ±12 V and ±5 V are also used. The input and output voltages are referenced to ground, and swing both positive and negative to a limit of VOM±, the maximum peak-output voltage swing.
A single-supply circuit (right side of Figure 1) connects the op-amp power pins to a positive voltage and ground. The positive voltage is connected to VCC+, and ground is connected to VCCor GND. A virtual ground, halfway between the positive supply voltage and ground, is the reference for the input and output voltages. The voltage swings above and below this virtual ground to the limit of VOM±. Some newer op amps have different high- and low-voltage rails, which are specified in data sheets as VOH and VOL, respectively. It is important to note that there are very few cases when the designer has the liberty to reference the input and output to the virtual ground. In most cases, the input and output will be referenced to system ground, and the designer must use decoupling capacitors to isolate the dc potential of the virtual ground from the input and output.

A common value for single supplies is 5 V, but voltage rails are getting lower, with 3 V and even lower voltages becoming common. Because of this, single-supply op amps are often rail-to-rail devices, which avoids losing dynamic range. Rail-to-rail may or may not apply to both the input and output stages. Be aware that even though a device might be specified as rail-to-rail, some specifications can degrade close to the rails. Be sure to consult the data sheet for complete specifications on both the inputs and outputs. It is the designer’s obligation to ensure that the voltage rails of the op amp do not degrade the system specifications.
1.2 Virtual Ground
Single-supply operation requires the generation of a virtual ground, usually at a voltage equal to Vcc/2. The circuit in Figure 2 can be used to generate Vcc/2, but its performance deteriorates at low frequencies.
In what follows, there are a few circuits in which a virtual ground has to be introduced with two resistors within the circuit because one virtual ground is not suitable. In these instances, the resistors should be 100 kW or greater; when such a case arises, values are indicated on the schematic.
1.3 AC-Coupling
A virtual ground is at a dc level above system ground; in effect, a small, local-ground system has been created within the op-amp stage. However, there is a potential problem: the input source and output load are probably referenced to system ground, and if the op-amp stage is connected to a source that is referenced to ground instead of virtual ground, there will be an unacceptable dc offset. If this happens, the op amp becomes unable to operate on the input signal, because it must then process signals at and below its input and output rails.
The solution is to ac-couple the signals to and from the op-amp stage. In this way, the input and output devices can be referenced to ground, and the op-amp circuitry can be referenced to a virtual ground.
When more than one op-amp stage is used, interstage decoupling capacitors might become unnecessary if all of the following conditions are met:
· The first stage is referenced to virtual ground.
· The second stage is referenced to virtual ground.
· There is no gain in either stage. Any dc offset in either stage is multiplied by the gain in both, and probably takes the circuit out of its normal operating range.
If there is any doubt, assemble a prototype including ac-coupling capacitors, then remove them one at a time. Unless the input or output are referenced to virtual ground, there must be an input-decoupling capacitor to decouple the source and an output-decoupling capacitor to decouple the load. A good troubleshooting technique for ac circuits is to terminate the input and output, then check the dc voltage at all op-amp inverting and noninverting inputs and at the op-amp outputs. All dc voltages should be very close to the virtual-ground value. If they are not, decoupling capacitors are mandatory in the previous stage (or something is wrong with the circuit).
1.4 Combining Op-Amp Stages
Combining op-amp stages to save money and board space is possible in some cases, but it often leads to unavoidable interactions between filter response characteristics, offset voltages, noise, and other circuit characteristics. The designer should always begin by prototyping separate gain, offset, and filter stages, then combine them if possible after each individual circuit function has been verified. Unless otherwise specified, filter circuits included in this document are unity gain.
1.5 Selecting Resistor and Capacitor Values
The designer who is new to analog design often wonders how to select component values.Should resistors be in the 1-W decade or the 1-MW decade? Resistor values in the 1-kW to 100-kW range are good for general-purpose applications. High-speed applications usually use resistors in the 100-W to 1-kW decade, and they consume more power. Portable applications usually use resistors in the 1-MW or even 10-MW decade, and they are more prone to noise. Basic formulas for selecting resistor and capacitor values for tuned circuits are given in the various figures. For filter applications, resistors should be chosen from 1% E-96 values. Once the resistor decade range has been selected, choose standard E-12 value capacitors. Some tuned circuits may require E-24 values, but they should be avoided where possible. Capacitors with only 5% tolerance should be avoided in critical tuned circuits— use 1% instead.
2 Basic Circuits
2.1 Gain
Gain stages come in two basic varieties: inverting and noninverting. The ac-coupled version is shown in Figure 3. For ac circuits, inversion means an ac-phase shift of 180°. These circuits work by taking advantage of the coupling capacitor, CIN, to prevent the circuit from having dc gain. They have ac gain only. If CIN is omitted in a dc system, dc gain must be taken into account.
It is very important not to violate the bandwidth limit of the op amp at the highest frequency seen by the circuit. Practical circuits can include gains of 100 (40 dB), but higher gains could cause the circuit to oscillate unless special care is taken during PC board layout. It is better to cascade two or more equal-gain stages than to attempt high gain in a single stage.
The traditional way of doing inverting attenuation with an op-amp circuit is shown in Figure 4, in
which R2 < R1. This method is not recommended, because many op amps are unstable at gains of less than unity. The correct way to construct an attenuation circuit1 is shown in Figure 5.
Attenuation values, the resistance R3 is:
· Select a base-value of resistance, usually between 1 kW and 100 kW for Rf and Rin.
· Divide Rin in two for RinA and RinB.
· Multiply the base value for Rf and Rin by 1 or 2, as shown in Figure 5.
· Look up the normalization factor for R3 in the table below, and multiply it by the base-value
of resistance.
For example, if Rf is 20 kW, RinA and RinB are each 10 kW, and a 3-dB attenuator would use a
12.1-kW resistor.
Noninverting attenuation can be performed with a voltage divider and a noninverting buffer as
shown in Figure 6.
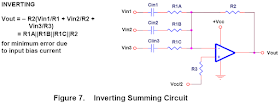
2.3 Summing Amplifier
An inverting summing circuit (Figure 7) is the basis of an audio mixer. A single-supply voltage is seldom used for real audio mixers. Designers will often push an op amp up to, and sometimes beyond, its recommended voltage rails to increase dynamic range. Noninverting summing circuits are possible, but not recommended. The source impedance becomes part of the gain calculation.
Just as there are summing circuits, there are also subtracting circuits (Figure 8). A common application is to eliminate the vocal track (recorded at equal levels in both channels) from stereo recordings.
The circuit in Figure 9 reverses the operation of a capacitor, thus making a simulated inductor. An inductor resists any change in its current, so when a dc voltage is applied to an inductance, the current rises slowly, and the voltage falls as the external resistance becomes more significant.
If a dc voltage is suddenly applied to the inverting input through resistor R1, the op amp ignores the sudden load because the change is also coupled directly to the noninverting input via C1.
The op amp represents high impedance, just as an inductor does. As C1 charges through R2, the voltage across R2 falls, so the op-amp draws current from the input through R1. This continues as the capacitor charges, and eventually the op-amp has an input and output close to virtual ground (Vcc/2). When C1 is fully charged, resistor R1 limits the current flow, and this appears as a series resistance within the simulated inductor. This series resistance limits the Q of the inductor. Real inductors generally have much less resistance than the simulated variety.
There are some limitations of a simulated inductor:
· One end of the inductor is connected to virtual ground.
· The simulated inductor cannot be made with high Q, due to the series resistor R1.
· It does not have the same energy storage as a real inductor.
The collapse of the magnetic field in a real inductor causes large voltage spikes of opposite polarity. The simulated inductor is limited to the voltage swing of the op amp, so the flyback pulse is limited to the voltage swing.
2.6 Instrumentation Amplifiers
Instrumentation amplifiers are used whenever dc gain is needed on a low-level signal that would be loaded by conventional differential-amplifier topologies. Instrumentation amplifiers take advantage of the high input impedance of noninverting op-amp inputs. The basic instrumentation amplifier topology is shown in Figure 10.
Here, the gain is easier to calculate, but a disadvantage is that now two resistors must be changed instead of one, and they must be matched resistors. Another disadvantage is that the first stage(s) cannot be used for gain. An instrumentation amplifier can also be made from two op amps; this is shown in Figure 12.
However, this topology is not recommended because the first op amp is operated at less than unity gain, so it may be unstable. Furthermore, the signal from Vin- has more propagation delay than Vin+.
This section is devoted to op-amp active filters. In many cases, it is necessary to block dc voltage from the virtual ground of the op-amp stage by adding a capacitor to the input of the circuit. This capacitor forms a high-pass filter with the input so, in a sense, all these circuits have a high-pass characteristic. The designer must insure that the input capacitor is at least 100 times the value of the other capacitors in the circuit, so that the high-pass characteristic does not come into play at the frequencies of interest in the circuit. For filter circuits with gain, 1000 times might be better. If the input voltage already contains a Vcc/2 offset, the capacitor can be omitted. These circuits will have a half-supply dc offset at their output. If the circuit is the last stage in the system, an output-coupling capacitor may also be required. There are trade-offs involved in filter design. The most desirable situation is to implement a filter with a single op amp. Ideally, the filter would be simple to implement, and the designer would have complete control over:
· The filter corner / center frequency
· The gain of the filter circuit
· The Q of band-pass and notch filters, or style of low-pass and high-pass filter (Butterworth,
Chebyshev, or Bessell).
Unfortunately, such is not the case— complete control over the filter is seldom possible with a single op amp. If control is possible, it frequently involves complex interactions between passive components, and this means complex mathematical calculations that intimidate many designers. More control usually means more op amps, which may be acceptable in designs that will not be produced in large volumes, or that may be subject to several changes before the design is finalized. If the designer needs to implement a filter with as few components as possible, there will be no choice but to resort to traditional filter-design techniques and perform the necessary calculations.
3.1 Single Pole Circuits
Single-pole circuits are the simplest filter circuits. They have a roll off of 20 dB per decade.
3.1.1 Low Pass Filter Circuits
Typical low-pass filter circuits are shown in Figure 13.
3.1.2 High Pass Filter Circuits
Typical high-pass filter circuits are shown in Figure 14.
The all-pass filter passes all frequencies at the same gain. It is used to change the phase of the signal, and it can also be used as a phase-correction circuit. The circuit shown in Figure 15 has a 90° phase shift at F(90). At dc, the phase shift is 0°, and at high frequencies it is 180°












No comments:
Post a Comment